» Home » Abul Wefa » Konstruktion des regulären Fünfecks, Variante 2 |
|
|
|
|
Konstruktion des regulären Fünfecks mit dem
"rostigen Zirkel" (rusty compass), Variante 2
nach Alfred Hoehn, 3/2003
Die hier vorliegende Methode zur Konstruktion eines regulären Fünfecks unter Zuhilfenahme eines rostigen Zirkels und eines Lineals wurde uns mit freundlicher Genehmigung von Alfred Hoehn zur Verfügung gestellt. Die Originalversion kann auf Alfred Hoehns persönlicher Webseite nachgelesen werden und zwar unter http://www.alfredhoehn.ch/Compass_Index.htm.
Hoehns zweite Methode zur Konstruktion eines
regulären Fünfecks beginnt mit der Betrachtung eines speziellen
rechtwinkligen Dreiecks mit Seitenlängen a, 2a und
![]() .
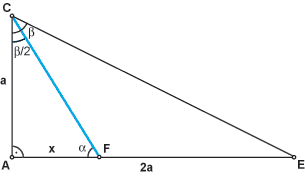
Trägt man die Winkelhalbierende des grösseren der beiden spitzen Winkel
ein, erhält man ein kleineres rechtwinkliges Dreieck, dessen Katheten
zueinander im Goldenen Schnitt stehen (Abb. 1).
.
Trägt man die Winkelhalbierende des grösseren der beiden spitzen Winkel
ein, erhält man ein kleineres rechtwinkliges Dreieck, dessen Katheten
zueinander im Goldenen Schnitt stehen (Abb. 1).
 |
|
Abb. 1 |
Wir wollen kurz überprüfen, ob dem tatsächlich so ist. Zunächst berechnen
wir den Winkel ACE, es sei dies β. Dann gilt:
.
Damit können wir die Strecke x = AF berechnen:
.
Im Dreieck AFC stehen somit die beiden Katheten im Goldenen Schnitt zueinander:
.
Die eben gewonnenen Erkenntnisse ermöglichen uns
eine Konstruktion des regulären Fünfecks mit dem rostigen Zirkel.
Die Konstruktion des Fünfecks
Wir beginnen mit der Konstruktion des rechtwinkligen Dreiecks AEC, dessen Katheten im Verhältnis 1 : 2 stehen. Dazu legen wir einen Kreisradius fest, den wir während der ganzen Konstruktion beibehalten werden und der gleichzeitig die Seitenlänge des regulären Fünfecks bestimmen wird.
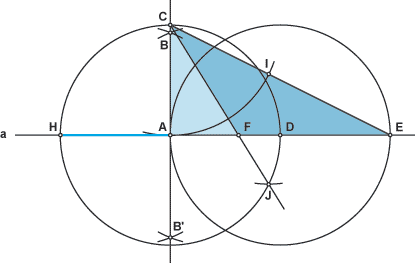
Als erstes zeichnen wir eine Gerade a. Danach konstruieren wir eine Senkrechte auf einen Punkt A, der auf der Geraden a zu liegen kommen soll. Dazu schlagen wir zwei Kreisbögen von zwei nahezu beliebigen Punkten auf a und erhalten die Schnittpunkte B und B'. Nun legen wir eine Gerade durch B und B' und schneiden diese mit a. Es resultiert daraus Punkt A, welcher die erste Ecke unseres gesuchten Fünfecks ist.
Indem wir einen Kreis um A schlagen, erhalten wir die Punkte C, D und H, wobei D und H auf der Geraden a liegen und C auf der Senkrechten durch A. H entspricht der zweiten Ecke unseres Fünfecks. Als nächstes schlagen wir einen Kreis um D und erhalten dadurch den Punkt E, welcher ebenfalls auf a liegt. Wir ziehen eine Gerade durch C und E und vervollständigen damit das rechtwinklige Dreieck AEC.
Nun gilt es, die Winkelhalbierende des Winkels ACE zu
finden. Dazu schlagen wir einen Kreisbogen um C. Dieser schneidet die
kleinere Kathete in A und die Hypotenuse in einem Hilfspunkt I. Da die
Winkelhalbierende durch den geometrischen Ort gehen muss, der gleich weit
von A und I entfernt ist, tragen wir einen Kreisbogen von I aus ab und
schneiden diesen mit dem Kreis um A. Es resultiert daraus der Hilfspunkt J.
Die Winkelhalbierende durch C und J schneidet die Strecke
AE in Punkt F.
|
|
|
Abb. 2 |
Abbildung 2 zeigt die beiden rechtwinkligen Dreiecke AEC und AFC, die sämtliche
Bedingungen erfüllen, die wir in der Vorbereitungsphase besprochen haben. Da das
Verhältnis AE : AC
= 2 : 1 ist und wir das Dreieck AFC aus der Winkelhalbierenden des Winkels ACE
konstruiert haben, folgt unweigerlich, dass die Strecken
AF und
AC zueinander im Goldenen Schnitt
stehen.
In der nächsten Phase wollen wir die noch verbleibenden drei Ecken des Fünfecks konstruieren. Wir beginnen mit einem Kreis um F und schneiden diesen mit dem Kreis um A. Schnittpunkt G entspricht der dritten Ecke unseres regulären Fünfecks. Wieso eigentlich? Das Dreieck AFG ist ein gleichschenkliges Dreieck, dessen Schenkel zur Basis ebenfalls im Goldenen Schnitt stehen. Denn es gilt offensichtlich AC = AG, weshalb auch AF und AG zueinander im Goldenen Schnitt stehen müssen. Für den Basiswinkel FAG des gleichschenkligen Dreiecks AFG lässt sich analog zur Variante 1 herleiten, dass dieser 72° ist. Der Winkel HAG ist somit 180° - 72° = 108°, was dem gewünschten Winkel im regulären Fünfeck entspricht.
Für den vierten Eckpunkt müssen wir die Mittelsenkrechte
von AH errichten. Dazu schlagen
wir einen Kreis um H und erhalten als Schnittpunkte mit dem Kreis um A die
Punkte M und M'. Der vierte Eckpunkt liegt nun auf der Geraden durch M und M'
und hat von G eine Radiuslänge Abstand. Wir tragen also von G aus einen
Kreisbogen ab, schneiden ihn mit der eben konstruierten Mittelsenkrechten und
erhalten dadurch den vierten Eckpunkt K. Von K aus tragen wir wiederum einen
Kreisbogen ab und schneiden ihn mit dem Kreis um A. Punkt L vervollständigt
unser reguläres Fünfeck (Abb. 3).
|
|
|
Abb. 3 |
| |
|
|
|
|
» Home » Abul Wefa » Konstruktion des regulären Fünfecks, Variante 2 |
|