» Home » Lorenzo Mascheroni » Konstruktion eines Quadrates

Konstruktion eines Quadrates

Zwei benachbarte Punkte sind gegeben

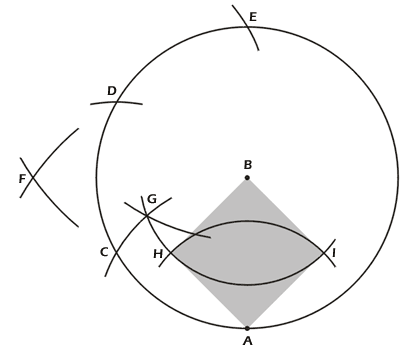
Gegeben seien die Punkte A und B (Abb. 1). Konstruiere die zwei fehlenden Ecken des Quadrates mit Seitenlänge AB. Mache dazu je einen Kreis mit Radius AB um die Punkte A und B. Diese Kreisbögen schneiden sich in C und F. Trage dann von C aus mit Radius AB zwei weitere Bögen ab, die den Kreis in D und E schneiden (wie schon in einem früheren Beispiel gezeigt wurde, liesse sich auch an dieser Stelle der Umweg über D vermeiden). Nimm nun CF in den Zirkel und trage von A und E aus je einen Bogen ab, woraus Schnittpunkt G hervorgeht. Danach machst du um A und B je einen Kreisbogen mit Radius BG, geschnitten mit den beiden anfänglichen Kreisen ergeben sich die Punkte H und I. Diese zwei Punkte sind die gesuchten Eckpunkte des zu konstruierenden Quadrates (grau unterlegt).
 

 
Beweis: Die Seite CF, die man benötigt um G zu erhalten, ist wiederum die Seite des gleichseitigen Dreiecks mit Umkreis B. Aus dem Beweis des vorangegangenen Beispiels (Napoleonisches Problem) folgt, dass AG = r sein muss. Mit Pythagoras berechnen wir die Diagonale des Quadrates ABIH mit Seitenlänge r:

Damit haben wir bewiesen, dass BG die Diagonale des Quadrates mit Seitenlänge r sein muss. 

 
Zwei diagonal gegenüberliegende Punkte sind gegeben

Gegeben seien die Punkte A und B, welche die Diagonale eines gesuchten Quadrates bilden (Abb. 2). Mache als erstes einen Kreis mit Mittelpunkt B und Radius AB. Trage mit demselben Radius von A aus die Punkte C, D und E auf dem Kreis ab. Trage zudem zwei Kreisbögen mit Radius AD von A und E ab. Der Schnittpunkt dieser beiden Bögen ist Punkt F (Aufgepasst: Im Mathematischen Zirkus von Martin Gardner ist dieser Punkt falsch eingezeichnet). Der Kreis mit Radius BF und Mittelpunkt E schneidet den Kreis mit Radius AB und Mittelpunkt A in Punkt G. Als nächstes trägst du von B und A aus je einen Kreisbogen mit Radius BG ab. H und I sind die Schnittpunkte dieser beiden Kreise. A, I, B und H bilden die Eckpunkte des gesuchten Quadrates, welches grau unterlegt ist.
 

 
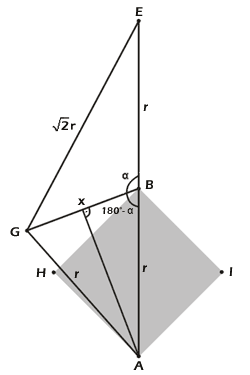
Beweis: Für den Beweis betrachten wir Abbildung 3. Wie wir bereits bewiesen haben, muss die Strecke EG = r sein, da sie gleich lang ist wie BF und wir dessen Länge schon zuvor mit dem gleichseitigen Dreieck bewiesen haben.

Die Strecke AB sei r und GB = x. Winkel GBE ist α, da die Punkte A, B und E auf einer Geraden liegen, ist Winkel GBA (180° - ). Mit dem Cosinussatz lässt sich für das Dreieck BEG folgende Gleichung aufstellen:

a² = b² + c² - 2bc(cos)

Das Dreieck AB(BG/2) ist rechtwinklig. Für den Winkel (180° - ) gilt also folgendes:

Wir setzen (II) in (I) ein und erhalten:

Wenn die Seiten des Quadrates die Länge besitzen, muss die Diagonale d = r sein. 

» Home » Lorenzo Mascheroni » Konstruktion eines Quadrates