» Home » Lorenzo Mascheroni » Mittelpunkt einer Strecke |
|
Mittelpunkt einer Strecke
In der heutigen Zeit besitzen die Mascheroni-Konstruktionen für die Geometer wenig Interesse. Da die Probleme jedoch unterhaltsamen Charakter haben, befassen sich zahlreiche Rätselliebhaber von neuem damit. Die Herausforderung besteht darin, die früheren Konstruktionen in weniger Schritten durchzuführen als der grosse Maestro. Dies ist teilweise möglich, wie wir schon beim nächsten Beispiel sehen werden. Mascheroni hat fünf verschiedene Methoden herausgefunden, um eine Strecke zu halbieren, hier die einfachste davon:
Mascheronis einfachste Lösung (Problem Nr. 66)
|
|
|
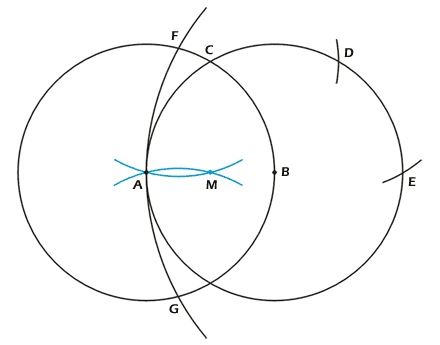
Abb. 1 |
Gegeben sind die Punkte A und B. Zeichne zuerst zwei Kreise
mit Radius AB um die Punkte A und
B. Trage mit derselben Zirkeleinstellung von C aus D ab und von D aus E. Der
neue Punkt E liegt auf der Verlängerung von AB
und ist doppelt so gross (siehe Einführung, Bsp. 1). Beschreibe
einen Kreis mit Mittelpunkt E und Radius AE.
Dieser Kreis geschnitten mit dem Kreis um Mittelpunkt A ergibt die Punkte F und
G. Trage nun von F und G aus je einen Kreisbogen mit dem Radius AB
ab. Der eine Schnittpunkt ist A, der andere unser gesuchte Mittelpunkt M der
Strecke AB.
Beweis: E liegt auf Grund der Konstruktion zwangsläufig auf der Verlängerung von AB, haben wir doch ansatzweise den Kreisumfang in sechs gleich grosse Bögen unterteilt. Die Punkte A, C, D und E sind somit Eckpunkte des regelmässigen Sechsecks mit Umkreis k(B, AB). Betrachten wir nun aber die beiden Dreiecke AFM und AEF: Beide sind gleichschenklig und haben den gemeinsamen Basiswinkel FAE. Daraus folgt, dass sie ähnlich sind. Wegen ihrer Ähnlichkeit sind ihre entsprechenden Seiten verhältnistreu.
Es lässt sich die Gleichung AE : AF = AF : AM aufstellen. Mit der Strecke AB ausgedrückt ergibt sich folgendes Verhältnis:
2AB : AB = AB : AM
Löst man diese Gleichung nach AM auf, erhält man:
AM = AB/2 (q.e.d)
Es
folgt, dass M der Mittelpunkt der Strecke AB
sein muss. ![]()
Verbesserte Mascheroni-Lösung
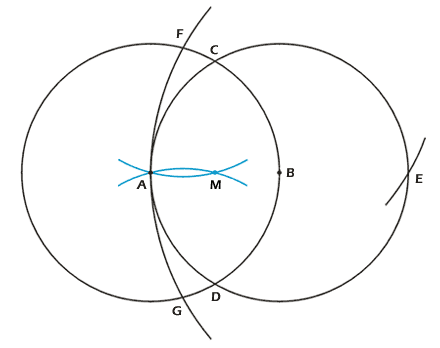
In Abbildung 2 zeigen wir, wie man die
Mascheronis Lösung von vorhin um einen Schritt verkürzen kann. Wiederum ist
der Mittelpunkt der Strecke AB,
die nur durch diese zwei Punkte gegeben ist, gesucht. Im Grunde genommen geht es
in dieser verbesserten Version um die genau gleiche Vorgehensweise wie vorhin,
nur dass man die Zahl der benötigten Kreisbogen auf 6 verringern kann. In der
vorhergehenden Konstruktion waren deren 7 nötig. In dieser Konstruktion kann
man sich den Umweg über den "alten" Punkt D ersparen. Das "neue"
D entspricht dem zweiten Schnittpunkt der Kreise um A und B. Die Strecke CD
ist gerade gleich lang wie die Strecke CE.
Die Punkte CDE bilden nämlich ein gleichseitiges Dreieck mit Umkreis k(B, AB).
Man trägt also einen Kreisbogen mit Radius CD
von C aus ab und erhält dadurch direkt Punkt E. Der Rest der Konstruktion sowie
der Beweis sind identisch. Diese neue Erkenntnis lässt sich bei vielen der
nachfolgenden Konstruktionen anwenden. ![]()
|
|
|
Abb. 2 |
Mascheronis komplizierteste Lösung
Wiederum wollen wir den Mittelpunkt einer
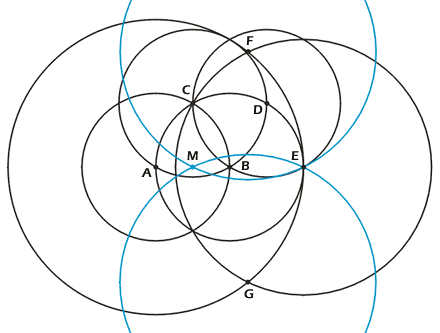
gegebenen Strecke AB (Abb. 3)
konstruieren. Diesmal jedoch auf eine kompliziertere Art und Weise. Zeichne
zuerst zwei Kreise mit Radius AB
sowie den Mittelpunkten A und B. Man erhält den Schnittpunkt C. Ziehe um C
einen weiteren Kreis mit Radius AB,
dies ergibt den Schnittpunkt D. Mache einen weiteren Kreis mit Radius AB
um D, woraus der Schnittpunkt E hervorgeht. Bis jetzt ist die Konstruktion
identisch mit der Konstruktion aus Abbildung 1. Selbstverständlich könnte man
auch hier wieder einen Schritt einsparen, indem man direkt zu Punkt E geht, ohne
den Umweg über D zu machen. Wir wollen uns aber an dieser Stelle auf den
weiteren Verlauf der Konstruktion konzentrieren, denn nun folgt die ultimative
Wende. Trage von E aus den Kreis durch C ab. Daraufhin machst du einen Kreis mit
Mittelpunkt A und Radius AE. Dort
wo sich die Kreise AE und EC
schneiden, liegen F und G. Zeichne nun zwei Kreise mit den Mittelpunkten G und F
sowie dem Radius EF. Unsere
beiden Kreise schneiden sich einerseits in E, andererseits im gesuchten
Mittelpunkt der Strecke AB.
|
|
|
Abb. 3 |
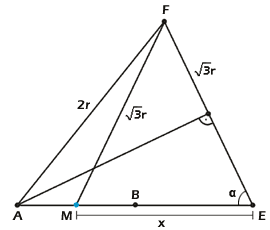
Beweis: Damit
der Beweis etwas anschaulicher wird, betrachten wir die Anordnung aus Abbildung
4 isoliert. Zunächst geht es um das Dreieck MEF. Die Strecke ME
sei das gesuchte x, EF und FM
sind je ![]() r, dies ist die
Seitenlänge des gleichseitigen Dreiecks mit Umkreis AB,
was wir später noch ausführlich beweisen werden. Man kann also mit dem
Cosinussatz folgende Gleichung aufstellen:
r, dies ist die
Seitenlänge des gleichseitigen Dreiecks mit Umkreis AB,
was wir später noch ausführlich beweisen werden. Man kann also mit dem
Cosinussatz folgende Gleichung aufstellen:
|
|
|
Abb. 4 |
Das Dreieck AE(EF/2) ist rechtwinklig, da es die Hälfte des gleichschenkligen Dreiecks AEF ist. Es gilt für α also folgende Gleichung:
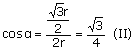
Gleichung II in I eingesetzt:
EM = ![]() r,
also BM =
r,
also BM = ![]() r.
Somit ist M der Mittelpunkt der Strecke AB.
r.
Somit ist M der Mittelpunkt der Strecke AB.
![]()
» Home » Lorenzo Mascheroni » Mittelpunkt einer Strecke |
|