» Home » Lorenzo Mascheroni » Mittelpunkt eines Kreises |
|
Mittelpunkt eines Kreises
Mascheroni hatte seiner Zeit auch das Problem gelöst, den
Mittelpunkt eines gegebenen Kreises aufzufinden. Seine Variante ist allerdings
sehr kompliziert und es gibt eine einfachere Methode, deren Herkunft unbekannt
ist, aber in vielen alten Büchern auftaucht (Abb. 1).
|
|
|
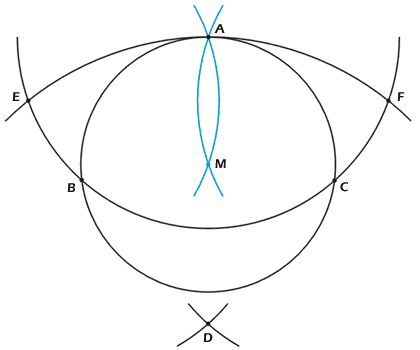
Abb. 1 |
Gegeben ist ein Kreis ohne Mittelpunkt. Wähle auf dem
Kreisbogen einen beliebigen Punkt A. Um A schlägst du nun einen Bogen mit dem
Zirkel, der den Kreis in B und C schneidet. Der Radius dieses Bogens ist frei wählbar,
er muss lediglich den Kreis in zwei Punkten schneiden, der Rest spielt keine
Rolle. Nun machst du zwei Bögen mit Radius AB
um B und C, sie schneiden sich in D. Der Punkt D kann nun inner- oder ausserhalb
des Kreises liegen, dies hängt lediglich von Radius AB
ab. Schliesslich ziehst du noch einen Kreisbogen mit Radius AD
um D. Geschnitten mit dem Kreisbogen um A ergeben sich die Punkte E und F. Der
letzte Schritt besteht darin, dass du von E und F aus je einen Bogen durch A
schlägst. Der zweite Schnittpunkt ist der gesuchte Mittelpunkt M.
|
|
|
Abb. 2 |
Beweis: Der folgende Beweis stammt von Marcel Gühr. Betrachte dazu nebenstehende Abbildung:
AM = x; BG = y
Dreieck AED ist ähnlich zu Dreieck AEM
G ist die Mitte von AD
==> AD = 2x + 2z
Behauptung: x = y
Beweis: (x + z)2 + h2 = r2; h2 = y2 - z2
==> x2 + 2xz + z2 + y2 - z2 = r2 (I)
==> r:x = (2x + 2z):r <==> 2xz = -2x2 + r2 (II)
(II) ==> (I): x2 - 2x2 + r2 + z2 + y2 - z2 = r2
==> - x2 + r2 + y2 = r2 <==> x = y
Damit ist die Behauptung bewiesen und M somit der
Mittelpunkt des Kreises. ![]()
» Home » Lorenzo Mascheroni » Mittelpunkt eines Kreises |
|