» Home » Konstruktionen mit Zahnstochern

Konstruktionen mit Zahnstochern

Kaum jemand weiss, dass alle Punkte, die man mit Zirkel und Lineal konstruieren kann, auch durch eine unbegrenzte Anzahl von gleich langen Zahnstochern erhalten werden können (Streichhölzer, Wattenstäbchen, usw. erzielen denselben Effekt). Zahnstocher sind dabei feste Strecken, die in der Ebene bewegt werden dürfen. Diese Konstruktionsmethode wurde von T. R. Dawson erfunden und im Kapitel "Match-Stick" Geometry (Streichholzgeometrie) in der Mathematical Gazette 1939 veröffentlicht. Dawson bewies, dass man nur Punkte konstruieren kann, die man auch mit Hilfe von Zirkel und Lineal erhalten kann. Die Herausforderung dieses Spiels ist es, Konstruktionen mit der kleinstmöglichen Anzahl von Zahnstochern zu vollführen.

 
Halbieren eines Winkels mit fünf Zahnstochern

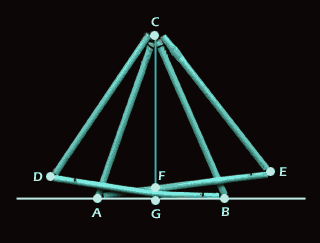
Gegeben sei ein Winkel ACB, der nicht grösser als 120° und nicht genau 60° ist, sowie eine Gerade durch die Punkte A und B. Gesucht ist der Mittelpunkt G von AB, den es nun mit Hilfe von gleich langen Zahnstochern zu konstruieren gilt (Abb. 1).
  

 
Nimm je zwei Zahnstocher und ergänze AB und BC zu einem gleichseitigen Dreieck. Du erhältst die Dreiecke ACE und BCD. Der Schnittpunkt dieser beiden Dreiecke ist F, er liegt auf der Winkelhalbierenden des Winkels ACB. Legt man nun einen fünften Zahnstocher durch C und F, ergibt sich der Schnittpunkt G mit dem Zahnstocher durch A und B.

 
Konstruktion eines Quadrates mit 16 Zahnstochern

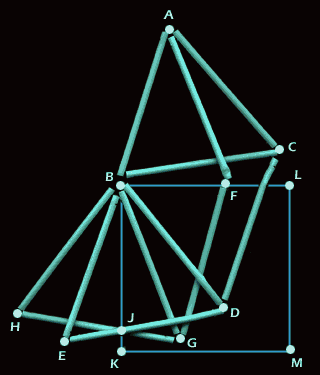
Bei diesem Beispiel geht es darum, ein Einheitsquadrat mit Kantenlänge gleich der Länge eines Zahnstochers zu konstruieren (Abb. 2). Fange irgendwo damit an, ein gleichseitiges Dreieck ABC zu bilden. Ergänze die Seite BC zu einem weiteren gleichseitigen Dreieck BCD, dasselbe tust du mit BD, es ergibt sich Dreieck BDE. AF ist eine beliebige Strecke innerhalb des Winkels BAC. Man erhält dadurch das gleichschenklige Dreieck ABF. "Spiegle" dieses Dreieck um BF, es folgt ein kongruentes Dreieck BFG. An die Strecke BG fügst du zwei weitere Zahnstocher an, so dass wir dort das gleichschenklige Dreieck BGH erhalten. Durch B und den Schnittpunkt J der Dreiecke BDE und BGH legst du die erste Seite des Quadrates (BK). Die Strecke durch B und F steht senkrecht dazu, dies ist unsere zweite Seite (BL). Nun ergänzt du das Quadrat mit zwei weiteren Zahnstochern, wobei sich Punkt M zwangsläufig ergibt – fertig ist unser Quadrat.
 

 
Begründung: Durch die Annahme des Winkels BAF ist eine Seite des Quadrates, nämlich die durch BF, bereits gegeben. Es gilt nun eine Senkrechte zu BF zu bilden, die gleichzeitig durch den Punkt B geht. Dies erzielt man, indem man das gleichschenklige Dreieck ABF "herunterspiegelt" und zwei weitere gleichseitige Dreiecke an ABC anfügt. Die Strecke AE ist dann 180° (Sechseck!). Der Winkel EBG ist dadurch gleich gross wie BAF, die Dreiecke BGE und ABF sind somit kongruent zueinander. Die Winkelhalbierende, die man nach derselben Methode wie im vorhergehenden Beispiel konstruiert, geht durch Punkt B und steht senkrecht auf BL.

 
Kommentar zu den Zahnstochern

In der Theorie mag die Streichholz-Geometrie ein amüsanter Zeitvertreib für Rätselliebhaber sein. In der praktischen Anwendung ergeben sich aber unerwartet grosse Probleme die Figuren mit Zahnstochern zu konstruieren. Ein grosses Mass an Konzentration und Fingerspitzengefühl sowie ein ausdauernder Rätselcharakter und starke Nerven sind wichtige Voraussetzungen zum praktischen Umsetzen der Theorie. Das ganze gerät oft zum Fiasko, da die Zahnstocher immer wieder verrutschen und sehr eigenwillig in ihrer Handhabung sind. Genaues Konstruieren ist somit schlichtweg unmöglich!

» Home » Konstruktionen mit Zahnstochern