Abul Wefa und der "rostige Zirkel"

» Home » Abul Wefa » Abul Wefa und der "rostige Zirkel"

Wie bereits erwähnt, beschäftigten sich schon die Griechen mit der Aufgabe, Konstruktionen auf eine möglichst elegante Art und Weise auszuführen. Einer angeblich auf Plato zurückgehenden Tradition zu Folge, stand bei ihnen die Konstruktion mit Zirkel und Lineal ganz zu oberst auf der Hitliste. In einem weiteren Schritt legten sich die Geometer der späteren Jahrhunderte noch schwerere Beschränkungen in der Wahl ihrer Instrumente auf. Ein Pionier auf diesem Gebiet war der persische Astronom und Mathematiker Abul Wefa Muhammad Ibn Yahya Ibn Ismail al-Buzjani (940-997 n. Chr.). Er lebte in Bagdad, Irak, wo er seine Kenntnisse über die Mathematik erlangte. Abul Wefa beschäftigte sich hauptsächlich mit der Trigonometrie und der Lösung von geometrischen Problemen mit der Zirkelöffnung. Er konstruierte auch Quadrate, die äquivalent zu anderen Quadraten waren, beschäftigte sich mit den Mondbewegungen und entdeckte die Variation.

In einem seiner Werke beschreibt er Konstruktionen, die mit Hilfe eines Lineals und eines "festen Zirkels" möglich sind. Abul Wefas "fester Zirkel" ist ein Zirkel, der seine Öffnung nie ändert, er wurde später in "rostiger Zirkel" umbenannt. Einfachere Beispiele für Konstruktionen mit Lineal und festem Zirkel sind die Methoden, eine Strecke oder einen Winkel zu halbieren.

Abb. 1

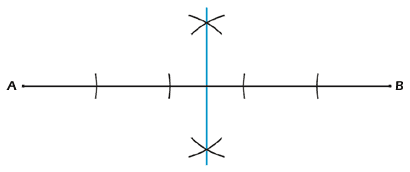
Abbildung 1 zeigt, wie man einen rostigen Zirkel benutzt, um eine beliebig lange Strecke zu halbieren. Man schlägt mit dem Zirkel von A und B je einen Bogen, schneidet diesen mit der Strecke AB und verkürzt damit die Strecke von beiden Seiten um den Radius der Zirkelöffnung. Von jetzt an wiederholt man diese Prozedur mit den neuen Schnittpunkten so oft, bis sich die Kreisbogen ober- und unterhalb der Strecke schneiden und erhält so die Mittelsenkrechte der Geraden AB.

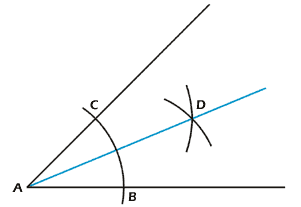
In Abbildung 2 wird gezeigt, wie man einen beliebig grossen Winkel (ungleich 180°) mit dem rostigen Zirkel halbiert. Man schlägt dazu einen Bogen um Punkt A und erhält damit die Punkte B und C. Man kann sich nun durch B und C eine Gerade vorstellen, deren Mittelsenkrechte man konstruieren muss. Man schlägt von B und C je einen Kreisbogen; der Schnittpunkt D der beiden Kreisbogen bildet mit Punkt A die Winkelhalbierende.

Abb. 2

Für die Konstruktion der "Winkelhalbierenden" eines gestreckten Winkels, also eines Winkels mit 180°, müssen zwei zusätzliche Schritte eingebaut werden (dasselbe gilt für 0°- bzw. 360°-Winkel, vorausgesetzt man will dort überhaupt etwas konstruieren):

Abb. 3

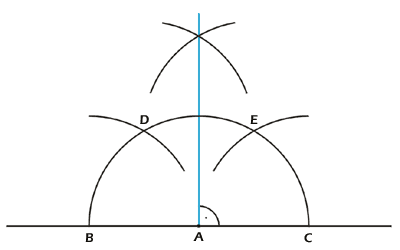
Man zieht mit dem rostigen Zirkel einen Halbkreis um A und erhält dadurch die Punkte B und C. Nun schlägt man um B und C je einen Kreisbogen und schneidet sie mit dem Halbkreis um A. Der Rest der Konstruktion bleibt dem vorhergehenden Beispiel gleich. Man verfährt mit D und E gleich wie mit B und C aus Abbildung 2. Die daraus hervorgehende "Winkelhalbierende" steht senkrecht auf der Geraden durch A. Man kann diese Konstruktion also auch dazu verwenden, um mit dem rostigen Zirkel einen 90° Winkel zu konstruieren.

Wir können die daraus gewonnenen Erkenntnisse bei unserer nächsten Konstruktion ganz gezielt einsetzen. Gegeben sei eine Gerade, gesucht ein Quadrat mit der Zirkelöffnung des rostigen Zirkels als Seitenlänge; eine Seite des Quadrates liege auf der Geraden. Die Lösung des Problems wird in Abbildung 4 gezeigt:

Abb. 4

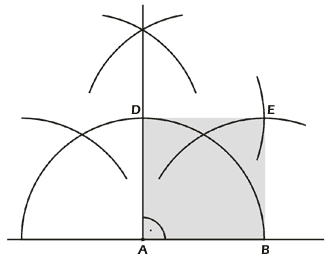
Man nehme irgendwo auf dieser Geraden einen Punkt A an und konstruiere nach demselben Prinzip wie in Abbildung 3 eine Senkrechte auf die Gerade. Dadurch erhält man automatisch die Eckpunkte B und D des Quadrates. Den vierten Punkt erhält man, indem man je einen Kreisbogen um die neu gewonnenen Punkte schlägt, der Schnittpunkt dieser beiden Kreisbogen muss die vierte Ecke C sein. Das resultierende Quadrat ist grau unterlegt.

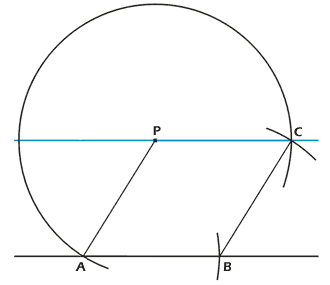
Der rostige Zirkel kann auch dazu benutzen werden, um eine Parallele zu einer Geraden durch einen beliebigen Punkt P ausserhalb der Geraden zu konstruieren (Abb. 5). Als erstes zeichnet man einen Kreis mit Mittelpunkt P, der die Gerade in A schneidet. Den Punkt B erhält man durch das Abtragen der Zirkelöffnung von A aus, nun zeichnet man einen weiteren Kreisbogen mit Mittelpunkt B, der Schnittpunkt mit dem ersten Kreis ergibt den Punkt C der Parallelen. Als Grundlage dieser Parallelenkonstruktion dient der Rhombus, dessen Ecken es zu konstruieren gilt, P ist eine davon. Alle vier Seiten eines Rhombus sind gleich lang, zudem sind die gegenüberliegenden Seiten jeweils parallel zueinander. Daraus folgt, dass die Gerade AB parallel zur Gerade PC sein muss.

Abb. 5

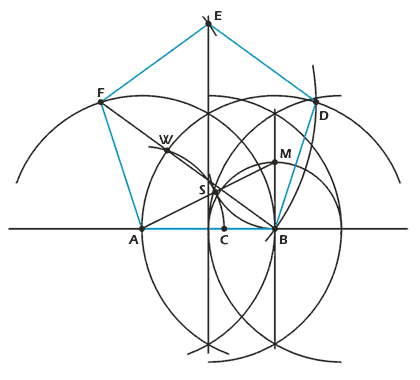
Abul Wefa soll laut Gardners Mathematischem Zirkus auch eine Methode gefunden haben, ein regelmässiges Fünfeck mit dem rostigen Zirkel zu konstruieren, wenn eine Seite gegeben ist. Leider führt Gardner die Konstruktion in seinem Buch nicht aus. Ein Vergleich zeigt allerdings, dass es schon relativ kompliziert ist, ein regelmässiges Fünfeck mit einem herkömmlichen Zirkel und Lineal zu konstruieren, wie Abbildung 6 illustrieren soll.

Abb. 6

Zum Vorgehen: Gegeben ist die Seite AB. Es gilt mit Hilfe des Goldenen Schnittes einen 36°-Winkel zu konstruieren. Dieser entspricht nämlich dem Basiswinkel der gleichschenkligen Dreiecke in einem Fünfeck, die sich aus zwei Seiten und einer Diagonale bilden lassen. Als erstes gilt es, die Seite AB mittels einer Mittelsenkrechten zu halbieren. Man schlägt dazu um A und B je einen Kreis, als Radius wählt man am besten gerade AB, da die beiden Kreise die geometrischen Orte der Punkte D und F des Fünfecks sind und man zu gegebener Zeit keine zusätzlichen Kreise machen muss. Man muss nun eine Senkrechte auf Punkt B konstruieren. Dies geschieht indem man einen Kreisbogen um den Mittelpunkt der Strecke AB zieht und ihn mit demjenigen Kreisbogen desselben Radius schneidet, dessen Mittelpunkt auf der Verlängerung von AB im Abstand AB/2 von B liegt. Punkt M liegt auf der Senkrechten durch B und zwar im Abstand AB/2 vom Punkt B entfernt. Das Dreieck ABM hat die idealen Voraussetzungen für den Goldenen Schnitt, der besagt AC : CB = AB : AC. Um Punkt C zu konstruieren (AC entspricht dann der Seitenlänge eines Zehnecks mit Umkreisradius AB), muss man zunächst von M aus einen Kreisbogen mit Radius MB ziehen und ihn mit der Strecke AM schneiden. Dies ergibt Punkt S. Mit Radius AS trägt man nun einen Kreisbogen um A ab, der AB in C und den Kreisbogen um Punkt A mit Radius AB im Punkt W schneidet. Ob man’s glaubt oder nicht, wir haben jetzt unseren gesuchten 36°-Winkel. Das Dreieck ABW ist ein Dreieck des Zehnecks mit Umkreisradius AB und Seitenlänge AC, der Winkel ABW ist also 36°! Die Gerade durch B und W ist nun eine Diagonale des gesuchten Fünfecks. Schneidet man diese mit dem Kreisbogen um A mit Radius AB erhält man den Eckpunkt F des Fünfecks. Nun fehlen uns noch zwei Eckpunkte. D erhält man, indem man von F aus einen Kreisbogen mit Radius FB schlägt und ihn mit dem Kreis um Punkt B mit Radius AB schneidet. Punkt E ergibt sich beinahe von selbst, er liegt auf der Mittelsenkrechten von AB, geschnitten mit dem Kreisbogen des Radius AB um die Punkte E oder F. Fertig ist unser regelmässiges Fünfeck!

Wer Interesse an einer Konstruktion des regulären Fünfecks mit rostigem Zirkel und Lineal bekundet, sei auf die nächsten beiden Seiten verwiesen. Dort stellen wir zwei Variante vor, die von Alfred Hoehn hergeleitet wurden. Sowohl Variante 1 als auch Variante 2 bedienen sich des Goldenen Schnittes als Ausgangslage für die Fünfeckskonstruktion.

Abb. 7

Nebst diesen konstruktiven Methoden gibt es eine viel einfachere Methode, ein regelmässiges Fünfeck herzustellen. Wir sagen absichtlich herstellen, weil es nämlich möglich ist, ein Fünfeck mit Hilfe eines Papierstreifens zu falten. Knüpft man einen gewöhnlichen Knoten in einen Streifen Papier mit parallelen Kanten und drückt diesen Knopf flach, erhält man ein regelmässiges Fünfeck, dies ist schon alt bekannt. Man nennt die Methode auch Le nœud de cravate (Abb. 7). Überhaupt lassen sich ganze Konstruktionen nur durch Faltungen ausführen.

Abb. 8

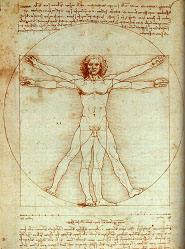
Jetzt aber wieder zurück zum rostigen Zirkel: Auch zahlreiche Mathematiker der Renaissance stellten Überlegungen zur Geometrie mit einem festen Zirkel an. Leonardo da Vinci, dieses Universalgenie, war einer davon. Schon in jungen Jahren zeigten sich seine aussergewöhnlichen Fähigkeiten in der Geometrie, Musik und Malerei. Sein hauptsächliches Interesse galt aber der Studie des Menschen. Viele seiner äusserst präzisen Zeichnungen über die Anatomie des menschlichen Körpers sind erhalten geblieben. Darunter auch jene, in der Leonardo den Körper eines Mannes mit der Form eines Kreises und eines Quadrates in Verbindung bringt und damit die Perfektion des menschlichen Körpers veranschaulichen will (Abb. 8). Dies soll nur ein Beispiel für seine fächerübergreifende Arbeitsweise sein.

Im Laufe der Zeit entwickelten sich die Konstruktionen mit dem rostigen Zirkel immer mehr zu mathematischen Spielereien. Der Londoner William Leybourn gab 1694 ein Buch mit dem Titel Pleasure with Profit heraus, in welchem er Konstruktionen mit dem rostigen Zirkel als eine Art mathematisches Spiel darstellt. Der folgende Abschnitt zeigt, wie er sich das vorgestellt hat: "Hier wird gezeigt, wie man (ohne Zirkel) nur mit Hilfe einer gewöhnlichen Gabel (oder eines ähnlichen Instrumentes, das sich weder weiter noch enger stellen lässt) und eines einfachen Lineals viele erfreuliche und reizende geometrische Operationen ausführen kann."

Im 19. Jahrhundert legte der französische Mathematiker Victor Poncelet den Grundstein für den Beweis, dass alle Konstruktionen mit Zirkel und Lineal bereits mit Lineal und einem festen Zirkel möglich sind. Der strenge Beweis wurde dann vom Schweizer Jacob Steiner durchgeführt.




» Home » Abul Wefa und der "rostige Zirkel"